Seguramente has escuchado decir a tu profesor muchas veces que el logaritmo de 0 no existe o que 0 no tiene logaritmo, pero quizás no sepas por qué.
He elaborado el presente escrito para ayudarte a comprender por qué cero no tiene logaritmo.

La explicación está basada en la definición del concepto de logaritmo de un número que trato primeramente.
¿Qué es el logaritmo de un número? ↑
El concepto de logaritmo de un número está relacionado con el concepto de potencia.
Potencia de un número ↑
Conoces que la potencia de exponente b de un número a se representa como a^b. Por ejemplo, 2^3 es la potencia de exponente 3 de 2 o tercera potencia de 2.
Quizás el uso de la frase “potencia de a” para nombrar la representación a^b provenga del significado que esta representación tiene cuando b es un número natural mayor que 1, pues cuando esto ocurre la potencia representa una multiplicación de a por sí mismo. Por ejemplo, 2^3=2\cdot 2\cdot 2=8.
Quien decidió utilizar esta denominación tal vez no se detuvo a pensar en los casos donde b es un número entero negativo, pues cuando ello ocurre lo que hace b es disminuir el número a cuando a\neq 1. Por ejemplo, 3^{-1}=\frac{1}{3}.
En la representación a^b, el número a se llama base y b exponente.
Obviamente, a^b es una representación de un tercer número que denotamos por c. Por esta razón, escribimos a^b=c y decimos que c es la potencia de exponente b del número a.
Logaritmo de un número ↑
Para representar el exponente utilizando la base y la potencia utilizamos el logaritmo. Por ejemplo, si tenemos la igualdad 2^5=32 y deseamos representar el exponente 5 utilizando la base 2 y la potencia 32, debemos utilizar la representación siguiente:
\log_{2} 32=5 En la igualdad anterior; 2 es la base, 32 es la potencia y 5 el logaritmo de 32 en base 2, es decir, el logaritmo es el exponente representado mediante la base y la potencia.Lo anterior indica que el nombre de los términos en una igualdad en la que interviene una potencia, su base y el exponente, depende de la representación (Tabla 1).
| Tabla 1: Nombre de los términos en potencias y logaritmos | |||
| Igualdad | Nombre de a | Nombre de b | Nombre de c |
| a^b=c | Base | Exponente | Potencia |
| \log_{a} c=b | Base | Logaritmo | Potencia |
La base de un logaritmo ↑
En la representación a^b el valor que puede tomar la base a depende del valor del exponente b. Pero si a es un número positivo, siempre existe la potencia a^b cualquiera sea b.
Por esta razón, el logaritmo se utiliza solo en casos de potencias de base positiva y en consecuencia la igualdad \log_{a} c=b significa a>0 y a^b=c; no solo a^b=c.
De las definiciones de potencia resulta que 1^b=1 para cualquier valor de b. De esta igualdad se obtienen las dos proposiciones siguientes:
- Cualquier número es el logaritmo de 1 en base 1.
- Ningún número, excepto 1, tiene logaritmo en base 1.
La primera proposición nos dice que el logaritmo de 1 en base 1 no es único, pero como deseamos que el logaritmo de un número sea único, debemos excluir el 1 como valor posible de la base.
La segunda proposición también es inconveniente porque deseamos que todo número positivo tenga logaritmo.
¿Por qué no existe el logaritmo de 0? ↑
De acuerdo con la regla presentada anteriormente que define el concepto de logaritmo de un número, la igualdad \log_{a} c=b significa a>0, a\neq 1 y a^b=c. Por tanto, c es una potencia de base positiva y en consecuencia siempre es positiva.
Esto indica que no existe exponente b tal que a^b=0 para a>0, es decir, no existe el logaritmo de 0.
La afirmación anterior es la respuesta a la pregunta del título de este escrito. Espero que la hayas comprendido. Si todavía te queda alguna duda o inquietud, puedes plantearla en la sección de los comentarios.
El logaritmo de cero en la matemática superior ↑
Quizás te hayas preguntado por qué nos interesamos por el logaritmo de cero si este no existe, pues un objeto que no existe no debiera acaparar nuestra atención.
El interés surge en la matemática superior cuando nos enfrentamos al cálculo de límites donde interviene una función logaritmo y especialmente la función logaritmo natural.
En el cálculo de límites es usual evaluar la función en el punto donde se calcula el límite y ahí es donde entra en juego el logaritmo de cero.
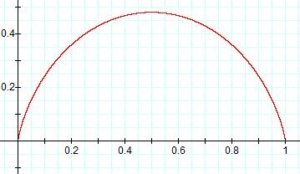
Por ejemplo, si deseamos calcular el límite \displaystyle\lim_{x \to 0}\ln x\ln(1-x), podemos intentar sustituir a x por 0 resultando el producto \ln0\cdot\ln1 que contiene el logaritmo natural de cero como factor.
Este caso es interesante porque a pesar de que f(x)=\ln x\ln(1-x) no está definida en cero porque el logaritmo natural de 0 no existe, el límite considerado sí existe y su valor es 0, según se observa en la imagen.
Notas finales sobre el logaritmo de 0 ↑
De la misma manera que he argumentado por qué 0 no tiene logaritmo, se pueden argumentar las respuestas a otras interrogantes.
Por eso, antes de concluir, quiero dejarte una pregunta para que trates de responderla de forma independiente.
Si te ha gustado este escrito en que te he explicado por qué no existe el logaritmo de 0, compártelo con tus amigos en las redes sociales.
Excelente. Me gustó mucho. Es una forma divertida de aprender. La matemática es hermosa. Te felicito por esa forma fácil de explicar las cosas.
Me alegro de que te haya gustado. Te invito a leer el escrito que explica por qué 0^0 no está definido. Puedes acceder desde aquí https://mathsandyou.com/cero-a-la-cero/
Instructivo para los que se inician en los logaritmos.